合成抵抗の計算方法|直列接続・並列接続はイメージで覚えよう
第二種電気工事士の筆記試験では、よく合成抵抗を計算する問題が出題されます。
合成抵抗の公式を覚えれば解ける問題ではありますが、真面目に考えて計算するのはやや面倒ですよね。そこで本記事では、合成抵抗の問題を効率的に解くテクニックをお伝えします。
なお「抵抗」そのものの解説はこちらの記事をご覧ください。
また日本エネルギー管理センターは最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策により、第二種電気工事士合格率が毎年90%以上を誇っています。
日本エネルギー管理センターの第二種電気工事士講習の詳細はこちらから
合成抵抗については動画でも解説しています。
目次
直列接続の合成抵抗の計算

直列接続の合成抵抗はシンプルです。上図のように直列で接続された複数の抵抗があるとき、直列接続の合成抵抗は各抵抗値をすべて足します。
仮にR1=3Ω、R2=2Ωだった場合、合成抵抗R=3+2=5Ωです。
あくまでイメージですが、直列接続の場合は「面積が同じとして抵抗の長さを延長する」といった考え方になります。
並列接続の合成抵抗の計算
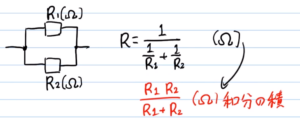
並列接続になると、合成抵抗の式は複雑になります。
- 抵抗が2つのとき:和分の積
- 抵抗が3つ以上のとき:各抵抗の逆数の和の逆数
仮にR1とR2が並列接続されている場合、合成抵抗Rは、R1の逆数とR2の逆数の和のさらに逆数を取ります(上図の黒字部分)。これを変換したものが、並列接続における合成抵抗の公式「和分の積」(上図の赤文字部分)です。
筆記試験では2つの抵抗を並列接続したものがよく出題されるので、和分の積は覚えておきましょう。
また、これもあくまでイメージですが並列接続の場合は「長さが同じとして面積を増やす」といった考え方になります。
合成抵抗の問題を効率的に解くテクニック
上述した直接・並列の合成抵抗の公式を覚えることは非常に重要です。
しかし、簡単なテクニックを覚えていれば、第二種電気工事士の問題はあっという間に解けてしまうものも少なくありません。とくに並列接続の合成抵抗の計算はこの傾向が顕著です。
そのテクニックとは「同じ値の抵抗をn個並列につなぐと、合成抵抗はn分の1になる」というものです。
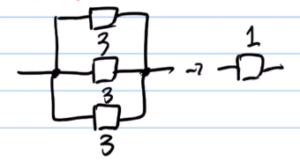
これを使うと「4Ωの抵抗が2個並列に接続されていたら2Ωになる」「3Ωの抵抗が3個並列に接続されていたら1Ωになる」と一瞬で計算できてしまいます。
不思議に感じた方は、ぜひ並列接続の合成抵抗の式で計算してみてください。
テクニックを覚えて効率よく計算しよう
第二種電気工事士の勉強をしていると、たくさんの公式が登場します。公式を覚え、その意味を理解することは重要ですが、試験において「いかに簡単に問題を解くか」も非常に重要になります。
第二種電気工事士では電卓の使用が禁止されているため、計算が複雑になるような数字は使われない傾向があります。過去問に取り組む際は、ぜひ今回ご紹介したテクニックを活用してみてください。
関連記事:第二種電気工事士を独学で合格する勉強方法|おすすめテキストも紹介
関連記事:筆記試験対策は早めに!効率良く勉強するポイントを紹介
日本エネルギー管理センターでは、最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策を提供しております。
第二種電気工事士合格率は毎年90%以上を誇ります。第二種電気工事士へ最短ルートでなりたい方は、ぜひ第二種電気工事士講習をご検討ください。



