「オームの法則」は水をイメージして覚えよう!分圧と分流についても解説
電気を勉強するうえで「オームの法則」は避けては通れない公式です。機械的に「V=IR」の式を覚えるのも一つの手ですが、もっと効果的に覚えるには水でイメージすることです。
本記事では水のたとえを使って「オームの法則」を初心者の方にもわかりやすく解説します。
なお「オームの法則」の前提知識である「電圧と電流」「抵抗」についても水にたとえて解説しています。
日本エネルギー管理センターは最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策により、第二種電気工事士合格率が毎年90%以上を誇っています。
日本エネルギー管理センターの第二種電気工事士講習の詳細はこちらから
またオームの法則については動画でも解説しています。
目次
オームの法則とは?水でイメージしよう
オームの法則とは「V=IR」で表される公式です。
- 電圧 V(V)
- 電流 I(A)
- 抵抗 R(Ω)
オームの法則を丸暗記で覚えるのも良いですが、水をイメージして覚えるとより式の概念が捉えやすくなります。
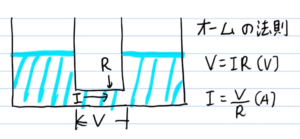
上図のような、配管でつながった2つのバケツをイメージしましょう。この図でたとえると、電圧、電流、抵抗の役割は以下になります。
- 電圧:左右の水圧差
- 電流:配管を流れる水の流量
- 抵抗:配管の流れにくさ
オームの法則を「I=V/R」に変換し、電流、つまり配管の流量に着目して考えてみます。
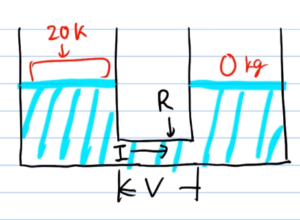
左側に水圧をかけると、配管内を左から右へ水が流れます。かける圧力を2倍にすれば、配管の流量も2倍に増えるはずです。
これは、電圧Vを大きくすれば電流Iも大きくなることと同じです。「I=V/R」の式の通りですね。
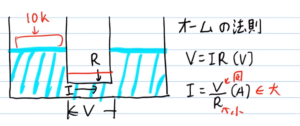
次に、かける水圧は同じまま、配管を太くしたらどうでしょうか。配管が流れやすくなるため、流れる水の量は増えますよね。
これは、電圧Vを一定にしたまま抵抗Rを小さくすると電流Iが増えることを意味します。これも「I=V/R」の式の通りです。
上記のようにオームの法則を水でイメージすると、公式が印象に残って覚えやすくなるのではないでしょうか。
オームの法則の実践問題!分圧と分流を解説
第二種電気工事士の筆記試験では、オームの法則が必要になる問題として「分圧」や「分流」に関する問題がよく出題されます。
- 分圧:直列接続において、電圧が各抵抗で分割されること
- 分流:並列接続において、電流が各抵抗で分割されること
それぞれについても水のたとえを使って解説します。
また分圧と電流については「オームの法則」の実践編として動画でも解説しています。過去問解説もしていますので、こちらもぜひご覧ください。
分圧の考え方
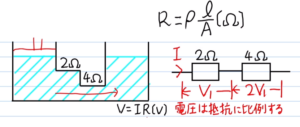
上図(右)のように、直列接続された2Ωと4Ωの抵抗それぞれにかかる圧力を考えてみましょう。
この回路を前項で使用した水のモデルで考えると、上図(左)のようになります。抵抗が小さい2Ωの部分は、水が流れやすい太い配管。4Ωの部分は細い配管のイメージです。
左側に圧力をかけると左から右に水が流れます。配管同士は接続されているので、流量は一定ですよね。
ただ同じ流量を流そうとすると、太い配管より細い配管のほうがより強い圧力を要するのが感覚的にわかるかと思います。
オームの法則「V=IR」をみると、電圧は抵抗に比例します。よって電流が一定のとき、4Ωにかかる電圧は2Ωにかかる電圧の2倍になり、これは水のイメージにおける「配管が流れ難いほど強い圧力が必要になる」と同じ意味合いになります。
分流の考え方
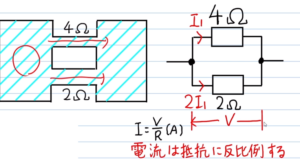
上図(右)のように、並列接続された4Ωと2Ωの抵抗にそれぞれ流れる電流を考えてみましょう。
水でイメージすると、この並列回路は、太さが異なる2本の配管が上図(左)のように並んで左右のバケツに接続されているのと同じです。
左側のバケツに圧力をかけた場合、それぞれの配管には同じ大きさの圧力がかかりますよね。ただ、2Ωの配管のほうが太いため、たくさん水が流れるはずです。
オームの法則「V=IR」→「I=V/R」をみると、電流は抵抗に反比例しています。電圧が一定のとき、4Ωの抵抗を流れる電流より、2Ωに流れる電流のほうが2倍大きくなるわけですね。
これは水のイメージにおける「圧力が同じなら、流れやすい配管のほうに水がたくさん流れる」と同じ意味合いになります。
(おまけ)短絡や開放についても考えてみよう
短絡(ショート)や開放についても水のイメージで考えられます。
短絡(ショート)の考え方

短絡とは、抵抗に何らかのトラブルが発生して0Ωに近い迂回路ができてしまった状態を指します。
電流、つまり水の流れになった気持ちで短絡した回路を見てみましょう。本来であればR1を通ってR2に流れるはずです。ただ、同じ区間にすごく流れやすい迂回路があったら、当然そこを通りたくなりますよね。
短絡を電気回路で表すと、抵抗R1が0Ωとの並列回路になったのと同じです。
和分の積で計算すると、並列部分の合成抵抗は0Ω。V=IRにより、R1にかかる分圧も0Vで、すべての電圧がR2にかかるようになります。
以上が短絡(ショート)の考え方です。
開放の考え方

開放は、上図(左)のように回路が途切れている状態を指します。
電圧はかかっているけれど回路がつながっていない状態ですので、抵抗5Ωに電流は流れません(電圧降下が発生しない)。これを水でたとえると、上図(右)のように配管が出口のところで塞がっているイメージになります。
水は流れませんが、配管に圧力はかかります。よって上図(左)の回路では「点aに電圧はかかっているけれど、5Ωの抵抗には電流が流れない」という状態になります。
オームの法則は基本の公式!納得して覚えよう
筆記試験の計算問題を解くうえで、オームの法則は基本の公式となります。公式をそのまま丸暗記するのも良いですが、公式のイメージを掴んでぜひ「納得して」覚えましょう。さまざまな問題へ応用が利きやすくなります。
関連記事:第二種電気工事士を独学で合格する勉強方法|おすすめテキストも紹介
関連記事:筆記試験対策は早めに!効率良く勉強するポイントを紹介
日本エネルギー管理センターでは、最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策を提供しております。
第二種電気工事士合格率は毎年90%以上を誇ります。第二種電気工事士へ最短ルートでなりたい方は、ぜひ第二種電気工事士講習をご検討ください。



