抵抗の面積と長さの関係を解説!抵抗の計算方法も
第二種電気工事士の筆記試験に合格するには「抵抗」について理解する必要があります。
どのテキストでも抵抗の解説にはページを割いていますが、はじめて電気を学ぶ人にとって抵抗のイメージを掴むのはなかなか難しいのではないでしょうか。
そこで本記事では、はじめて電気を学ぶ初心者の方に向けて、抵抗についてわかりやすく解説します。
なお日本エネルギー管理センターは最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策により、第二種電気工事士合格率が毎年90%以上を誇っています。
日本エネルギー管理センターの第二種電気工事士講習の詳細はこちらから
また抵抗については動画でも解説しています。
目次
抵抗とは?
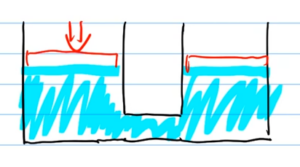
上図のような、配管でつながった2つのバケツがあるとします。
電圧と電流を水で例えると、電圧は「左右のバケツの水圧差」、電流は「配管を1秒間に流れる水の流量」になりますよね。左右のバケツの水圧が同じであれば水は流れませんが、左のバケツの水面を上から押して圧力をかければ、左から右に水が配管を通って流れるはずです。
「抵抗」は上図における「配管の水の流れ難さ」を意味します。
配管が細いほど、また配管が長いほど水は流れにくくなる……つまり、抵抗が大きくなるわけです。このイメージを念頭に、抵抗の公式を見てみましょう。
抵抗の公式
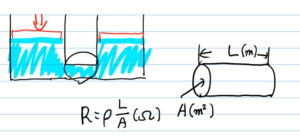
抵抗Rの公式において、Aは電線の断面積、Lは電線の長さ、ρは電線の抵抗率を表します。上図でいうとAは配管部分の断面積、Lは配管の長さ、ρは配管の材質ですね。
たとえば配管の断面積Aが2倍になれば、水が2倍流れやすくなります(抵抗の大きさは2分の1になる)。また配管の表面がツルツルした材質より、ザラザラしている材質のほうが流れにくいはずです(抵抗率が大きいほど抵抗の値は大きくなる)。
上記のように公式の構成要素もイメージで捉えると抵抗の公式も覚えやすいかと思います。
余談ですが身近な金属の抵抗率は「銀→銅→金→アルミ」の順に大きくなります。電線に銅がよく使われるのは、銀より安価で電流が流しやすいためです。
断面積の考え方

抵抗の問題を解くときにポイントとなるのが断面積Aです。問題が断面積ではなく電線の直径や半径で与えられ、円の面積の式と抵抗の式のどちらも知っていないと解けない問題がよく出題されます。
「円の面積=半径×半径×円周率π」です。つまり、電線の直径が2倍になったら面積は4倍になり、抵抗値は4分の1になります。逆に面積が2分の1になったら、面積は4分の1になるので、抵抗値は4倍になります。
覚えておくと便利!直径と面積の定番パターン

抵抗の問題を解く際に、覚えておくと便利な直径と面積の定番パターンをご紹介します。
電線の直径には決まりがあります。よって、筆記試験でよく出てくる数字の組み合わせはだいたい上図の4つです。直径D=1.6mmのとき断面積A=2mm^2、直径Dが2倍の3.2mmになると断面積は4倍の8mm^2になる……というわけですね。
円の面積の式は覚えておいて損はありません。ただ紹介した4パターンを覚えておくと、いちいち計算しなくても問題が解けてしまうことがあります。

たとえば上記のような問題では直径2.6mm×長さ10mの電線が登場します。直径2.6mmの断面積は5.5mm^2ですので、答えはイです。
数字を覚えておくだけで、計算問題にかかる時間を節約できます。ぜひ活用してください。
抵抗のイメージを掴んで計算問題を解けるようになろう
第二種電気工事士の筆記試験では、最初の1〜8問目くらいまで計算問題が出題され、そのなかに抵抗の公式を使って解く問題がよく登場します。
ただ、問題の使用される数字にはパターンがあり、抵抗のイメージと定番パターンを知っているだけであっさり解けてしまう問題も少なくありません。
計算問題が苦手な方もいらっしゃるかと思いますが、ぜひ本記事を参考に、抵抗の問題で正解できるようにしてください。
関連記事:第二種電気工事士を独学で合格する勉強方法|おすすめテキストも紹介
関連記事:筆記試験対策は早めに!効率良く勉強するポイントを紹介
日本エネルギー管理センターでは、最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策を提供しております。
第二種電気工事士合格率は毎年90%以上を誇ります。第二種電気工事士へ最短ルートでなりたい方は、ぜひ第二種電気工事士講習をご検討ください。



