第二種電気工事士の筆記試験ではいくつか計算問題が出題されますが、電卓の持ち込みが禁止されているため、手計算する必要があります。

そこで本記事では、交流の計算問題を解くときに覚えておきたい基礎知識「三平方の定理」について解説します。

なお日本エネルギー管理センターは最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策により、第二種電気工事士合格率が毎年90%以上を誇っています。

日本エネルギー管理センターの第二種電気工事士講習の詳細はこちらから

「三平方の定理」とは？

「三平方の定理」とは、直角三角形の3つの辺 a、b、c（cは斜辺とする）において成立する以下の定理です。

たとえば「2辺の長さが3 cmと4 cm、斜辺の長さが5 cm」のとき、上式の左右の項はどちらも25となり、三平方の定理が成り立ちます。

では筆記試験のどこで三平方の定理を活用するかというと、交流回路の計算です。ただ、三平方の定理をそのまま活用するというよりは、以下の3つの直角三角形を覚えて活用します。

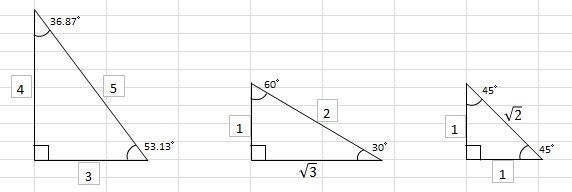
「3:4:5」「√3：１：２」「１：１：√２」の直角三角形は三平方の定理で定番です。いずれも三平方の定理が成立していますので、興味のある方は計算してみてください。

第二種電気工事士の筆記試験では、この3種類の数字の組み合わせを暗記しておくだけでほとんどの問題に対応できます。とくに「3：4：5」の直角三角形は使用頻度が高くなりますので、これだけでも覚えておくことをおすすめします。

「三平方の定理」の活用方法

三平方の定理を活用するといっても、文章だけではよくわかりませんよね。実際の問題を解いてみましょう。

問：抵抗（１２Ω）と誘導性リアクタンス（１６Ω）の直列回路がある。この回路の合成インピーダンスを求めよ。

公式通りにやるならば、「12と16をそれぞれ二乗し、その和のルートをとる」ことになります。しかし、2桁の乗数を手計算するのはやや煩雑です。

そこで、三平方の定理を活用します。

底辺が3、高さが4の直角三角形は、斜辺が5になりますよね。詳しくはテキストを参照いただきたいのですが、じつは抵抗とリアクタンスをベクトルで書くと、まさに底辺が抵抗、高さがリアクタンスになります。

そうすると、底辺が12、高さが16ですから3：4の比になっています。この比で考えると斜辺は5にあるはずですから、3：4：5＝12：16：20ということで合成インピーダンスは20Ωと求められます。

文章で書くと長くなってしまいますが、要するに3：4だから合成は5と考えているだけなのです。

なお三平方の定理が活用できる計算問題については、以下の動画で紹介・解説しています。実際に解いている様子がわかりますので、ぜひ参考にしてください。

三平方の定理で計算問題を効率的に解こう！

筆記試験の過去問を見てみると、とくに3：4：5の直角三角形が活用できる計算問題が非常によく出てきます。

三平方の定理および直角三角形の比を知っていれば、暗算で効率的に計算問題を解けるようになります。ぜひ活用してください。

また、第二種電気工事士の試験対策については以下の記事で詳しく解説していますので、ぜひこちらもご一読ください。

関連記事：第二種電気工事士を独学で合格する勉強方法｜おすすめテキストも紹介

なお日本エネルギー管理センターでは、最短かつ最小の労力で合格を目指せるノウハウと、徹底した技能試験対策を提供しております。

第二種電気工事士合格率は毎年90%以上を誇ります。第二種電気工事士へ最短ルートでなりたい方は、ぜひ第二種電気工事士講習をご検討ください。

日本エネルギー管理センターの第二種電気工事士講習はこちらから